ЗАДАЧА№1
Построить проекции равнобедренного прямоугольного треугольника АВС, если известно, что катет ВС принадлежит прямой KL.
Исходными данными задачи является точка А – вершина треугольника и прямая KL, на которой расположен его катет ВС. Прямая KL – линия уровня (параллельна плоскости проекций П1 или П2).
РЕШЕНИЕ:
1) По заданным координатам в таблице с вариантами строим проекции точек А, Р и прямой KL, в нашей задаче KL параллельна П1 – т.е. горизонталь (координаты по оси z равны 30).
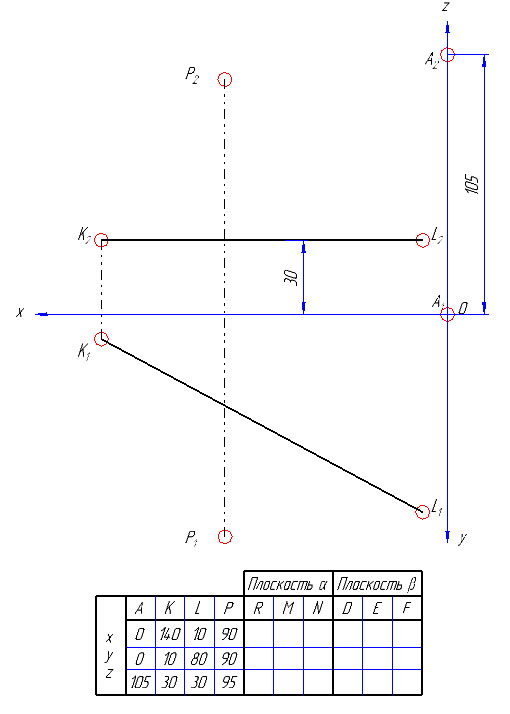
2) Из точки А опускаем перпендикуляр на прямую KL (так как искомый треугольник прямоугольный, а вершина А задана).
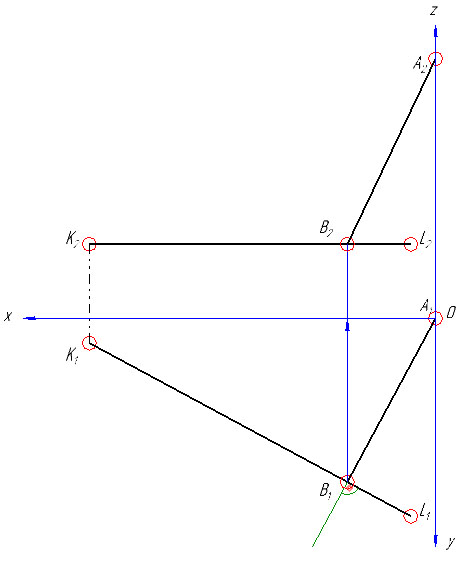
Отмечаем основание перпендикуляра – точку В (В1). Фронтальную проекцию точки В (В2) получаем по линии связи на К2L2.
3) Определяем натуральную величину катета АВ треугольника АВС способом прямоугольного треугольника: для этого на фронтальной проекции берем отрезок равный разнице координат проекций точек А и В – дельта z, и под прямым углом к горизонтальной проекции отрезка AB (A1B1) откладываем отрезок равный дельта z, получаем точку А0. В1А0 – будет натуральной величиной катета (отрезка) АВ.

4) На прямой KL от точки В в любую сторону откладываем натуральную величину катета АВ (так как в равнобедренном прямоугольном треугольнике оба катета равны). В нашем случае откладываем на горизонтальной проекции K1L1 – т.к. KL – горизонталь и проецируется в натуральную величину именно на плоскость П1. Получаем точку С (сначала проекцию С1 и по линии связи C2).

Соединяем точку А с точкой С. Треугольник АВС – искомый.
ЗАДАЧА№3
Определить натуральную величину расстояния от точки Р до плоскости.
РЕШЕНИЕ:
Кратчайшим расстоянием от точки до плоскости является отрезок перпендикуляра.
1) На основании теоремы о перпендикуляре к плоскости горизонтальная проекция перпендикуляра из точки Р проводится перпендикулярно к горизонтальной проекции горизонтали h. Независимо от горизонтальной проекции строится его фронтальная проекция. Для этого по плоскости найденного треугольника АВС проведена фронталь ƒ. Фронтальная проекция перпендикуляра должна быть перпендикулярна фронтальной проекции фронтали ƒ.
2) Прямая перпендикуляра из точки Р заключена в горизонтальнопроецирующую плоскость γ1. Затем определена линия пересечения 2-3 вспомогательной плоскости γ с заданной плоскостью треугольника АВС.

В пересечении линии 2-3 с прямой n найдена искомая точка Q. Сначала определяется фронтальная проекция Q2, а затем по линии проекционной связи определена ее горизонтальная Q1 проекция.

3) Натуральная величина перпендикуляра PQ определена способом прямоугольного треугольника, аналогично как в задаче №1 определяли натуральную величину катета АВ.

Эпюра с задачами 1 и 3 — вариант 24
ЗАДАЧА №2.
Построить линию пересечения двух плоскостей заданных треугольниками α(DEF) и β(RMN), координаты вершин которых заданы в таблице исходных данных.
РЕШЕНИЕ:
1) По заданным координатам строим проекции всех точек, получаем проекции треугольников DEF и RMN.
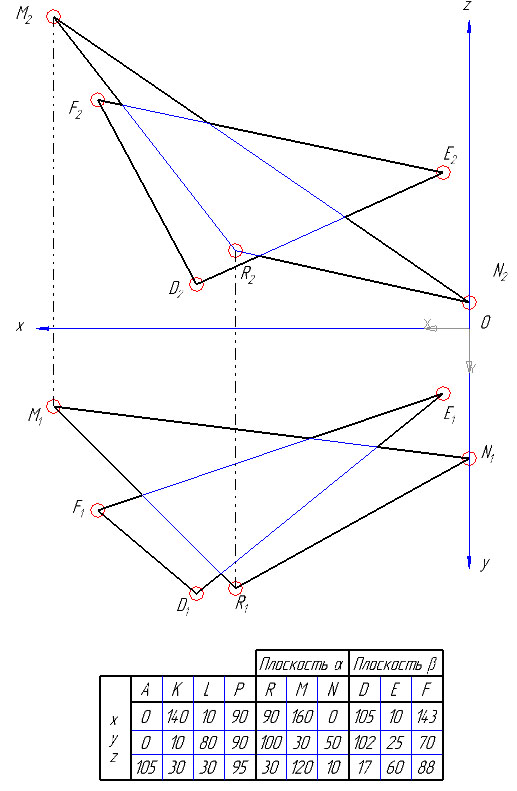
2) Решение задачи можно упростить, если вспомогательные проецирующие плоскости провести через прямые, задающие плоскость.
Так точка K этой линии определена с помощью горизонтальнопроецирущей плоскости δ1, проведенной через сторону RM треугольника MNR. Именно линия RM является линией пересечения плоскости треугольника β(RMN) с вспомогательной плоскостью δ. Та же плоскость пересекает треугольник α(DEF) по линии 1-2.
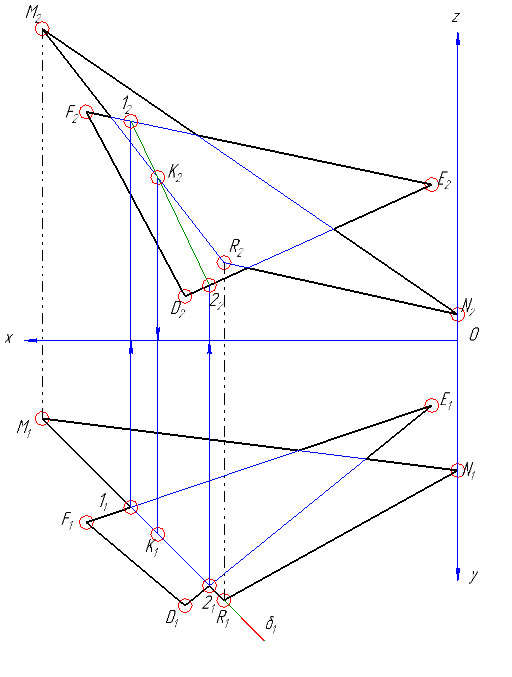
Точка K, общая для трех плоскостей (двух заданных α и β и вспомогательной δ), находится в пересечении прямых 1-2 и RM.
Следует отметить, что если вспомогательная плоскость δ горизонтальнопроецирущая, то сначала определяется фронтальная проекция точки K2, т.е. K2 = 12-22∩R2M2, а затем по линии проекционной связи находится K1 – горизонтальная проекция точки K.
3) Аналогично, заключая сторону DE во фронтальнопроецирующую плоскость γ2, находится точка L. Прямая KL – линия пересечения заданных плоскостей.

4) Для определения видимости этих треугольников достаточно установить относительное расположение одной из сторон одного треугольника относительно стороны другого треугольника. Таким образом, вопрос видимости плоскостей сводится к определению видимости двух скрещивающихся прямых.

Определим видимость стороны DE треугольника DEF относительно стороны MN треугольника RMN на фронтальной плоскости проекции. Для этого проведем луч зрения s перпендикулярно П2 через точку пересечения фронтальных проекций D2E2 и M2N2. В пересечении D2E2 и M2N2 расположены две конкурирующие по видимости точки (52 и 42). Точка 4 принадлежит стороне MN, а точка 5 – стороне DE. По горизонтальной проекции устанавливаем, что луч зрения сначала встретит D1E1 в точке 51, а затем M1N1 в точке 41. Следовательно, фронтальная проекция D2E2 – видима.

Аналогично определяется видимость треугольников и на горизонтальной проекции. Луч зрения при этом следует провести перпендикулярно к П1 через две конкурирующие на П1 точки скрещивающихся прямых (например, луч s/, проходящий через точки 1 и 6, соответственно принадлежащие прямым MR и ЕF).

Эпюр с задачей №2
ЗАКАЗЫВАЙТЕ ЧЕРТЕЖИ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ МГУПС
тел. (whatsup) 8-950-790-65-90
email: stud-help55@ya.ru
Раздел: Начертательная геометрия /







