тел: +7 (950) 790-65-90 - Алексей
Задача: В плоскости, заданной следами, взять произвольный отрезок АВ. Способом совмещения определить его истинную величину. Принимая отрезок за сторону правильной плоской фигуры (квадрат), построить эту фигуру.
Теория
Способ совмещения заключается в том, что заданную плоскость а (альфа) вместе с расположенными в ней геометрическими элементами вращают вокруг одного из ее следов foa или hoa до совмещения с соответствующей плоскостью проекций Н или V.
Все геометрические элементы (прямые и другие линии, фигуры), лежащие в заданной плоскости, изображаются в натуральную величину на плоскости проекций, с которой производится совмещение. Совмещение позволяет найти величину плоской фигуры по ее проекциям или построить проекции плоской фигуры, лежащей в какой-либо плоскости, по заданным ее размерам.
Пошаговое решение:
1) Берем произвольную проекцию точки В (B») во фронтальной плоскости V, находим ее проекцию B’ горизонтальной плоскости проекций Н, из у словия, что отрезок АВ лежит в плоскости альфа.
2) Т.к. плоскость задана следами, то задача совмещения ее с плоскостью проекций сводится к построению совмещенного положения одного из следов — fo1a, так как другой след — hoa, принимаемый за ось вращения, не меняет своего положения.
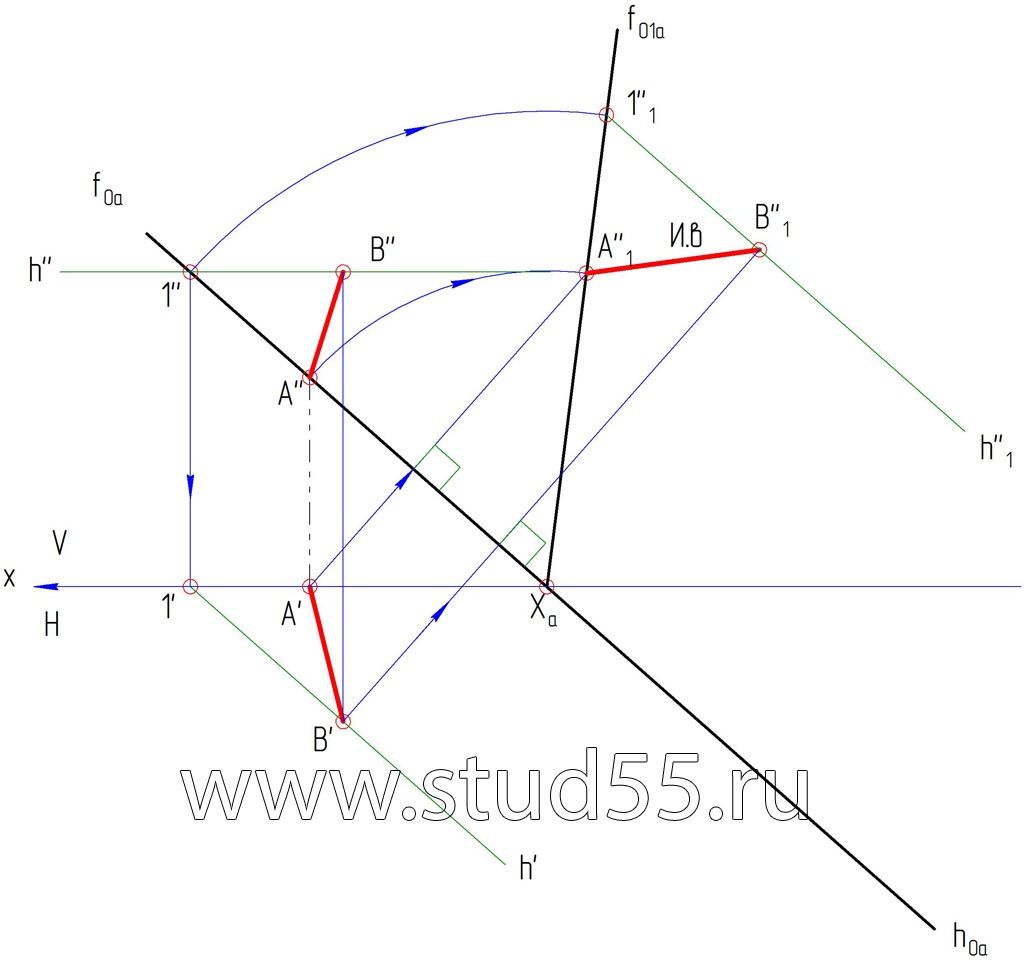Отрезок АВ, лежащий в заданной плоскости, изображается в истинную величину (И.в.) на новой плоскости проекций, с которой мы произвели совмещение.
3) В совмещенной плоскости достраиваем искомую фигуру (квадрат со стороной АВ).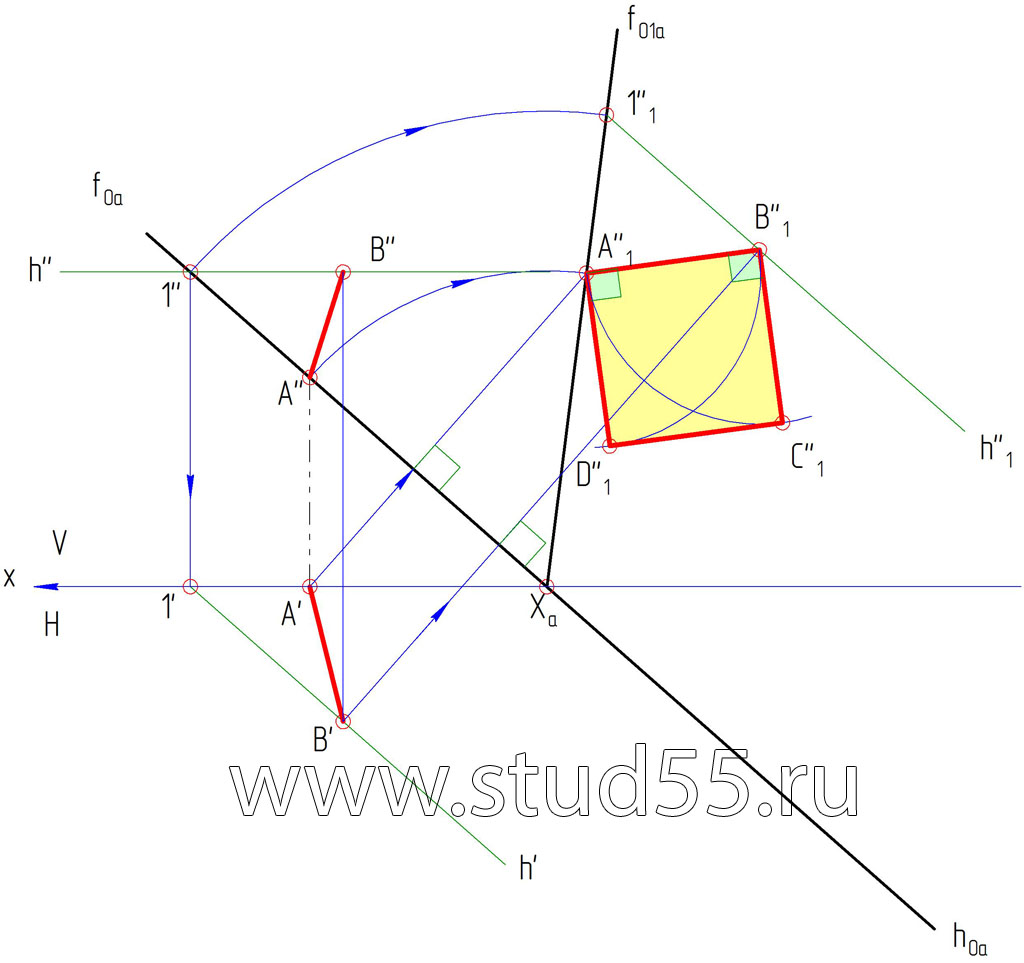
4) В совмещенной плоскости проводим горизонталь через проекцию точки D ( D»1), обратным вращением при помощи точки 2, находим горизонталь в плоскостяи проекций V, затем в H, а также проекции точки D — D’, затем по линии связи — D».
5) Проекции точки С (С» и C’) можно найти аналогичным способом, также как и нахождение точки D, или простыми построениями параллелограммов (квадрат отображается в виде параллелограмма).
У кого есть вопросы, пишите в комментариях!
Раздел: Начертательная геометрия /
